Combien de bords a un prisme pentagonal?
Pouvoir compter Combien de bords un prisme pentagonal a-t-il?, les concepts "bord" (bord d'un objet), "prisme" (figure géométrique) et "pentagonal" (par rapport à la forme d'une figure géométrique) doivent être compris.
Quand on parle de pentagonal, la première chose à penser est que le préfixe "penta" indique que le personnage doit avoir cinq côtés. Par conséquent, la figure doit avoir une forme similaire à celle d'un pentagone.

Un "bord" est un bord d'un objet. Géométriquement, c'est une ligne qui relie deux sommets consécutifs d'une figure géométrique.
Un "prisme" est une figure géométrique limitée par deux bases, qui sont des polygones égaux et parallèles, et dont les faces latérales sont des parallélogrammes.
Dans l'image montrée au début, les faces latérales du prisme pentagonal sont des rectangles. Ceci n'est qu'un cas particulier, car la définition indique que ses faces latérales sont des parallélogrammes.
Cela permet de classer les prismes comme "droits" et "obliques".

Pour connaître le nombre d'arêtes d'un prisme pentagonal, le type de prisme avec lequel on travaille n'a pas d'importance. Que ce soit droit ou oblique, le nombre d'arêtes ne changera pas.
Façons de compter les arêtes d'un prisme pentagonal
1- Premier formulaire
Comme les bases des prismes pentagonaux sont des pentagones, chaque base a cinq arêtes.
D'autre part, à partir de chaque sommet d'un pentagone, une arête est projetée sur le sommet correspondant de l'autre pentagone; c'est-à-dire qu'il y a cinq arêtes qui se rejoignent l'une avec l'autre.
En ajoutant toutes les arêtes, nous obtenons un total de 15 arêtes.
2- Deuxième forme
Une autre façon de compter les arêtes consiste à décomposer le prisme pentagonal dans ses deux bases et ses faces latérales. Cela permettra d'obtenir deux pentagones et un parallélogramme avec quatre lignes intérieures.

Chaque pentagone a cinq bords. Par contre, à première vue, on pourrait se tromper en disant que le parallélogramme contient huit arêtes (six verticales et deux horizontales). Mais ce raisonnement devrait être mieux analysé.
Si toutes les lignes verticales sont comptées, il est à noter que la première ligne à gauche sera jointe à la dernière ligne à droite, avec laquelle les deux lignes représentent un seul bord. Mais qu'en est-il des deux lignes horizontales?
Lorsque toutes les pièces seront rassemblées, les lignes horizontales seront jointes, chacune avec les cinq bords de chaque pentagone. Pour cette raison, les compter séparément serait une erreur.
Le parallélogramme contient donc cinq arêtes du prisme qui, avec les 10 arêtes comptabilisées au début, donnent un total de 15 arêtes.
Autres types de prisme
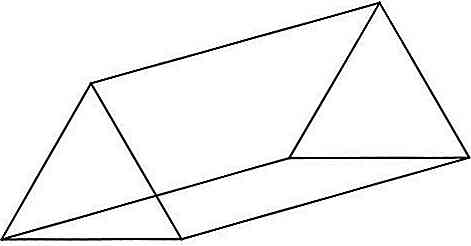
Prisme triangulaire
Ce sont des prismes dans lesquels les bases sont des triangles et le nombre d'arêtes est de 9.
 Prisme quadrangulaire
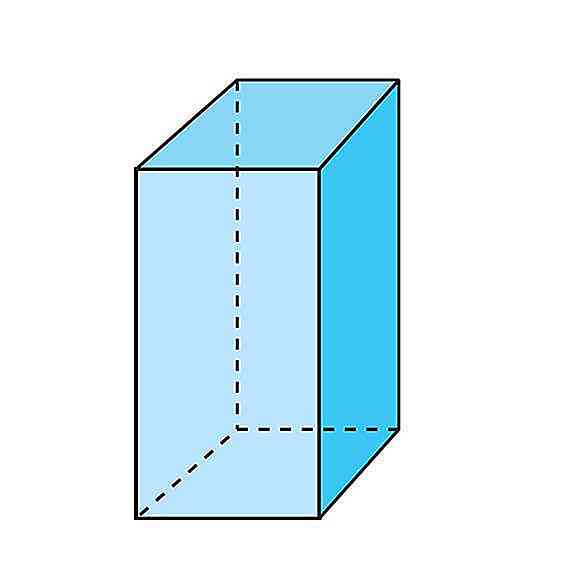
Prisme quadrangulaire
Les bases de ces prismes sont des quadrilatères et le nombre d'arêtes est de 12.
 Prisme hexagonal
Prisme hexagonal
Les bases sont des hexagones et le nombre d'arêtes est de 18.

Comme on peut le voir dans les autres types de prisme, le nombre d'arêtes peut être déduit par une formule mathématique: il serait égal à 3 multiplié par le nombre de côtés que possède l'une des bases.
Comme il a été dit précédemment, un prisme peut être droit ou oblique, mais en plus il existe des prismes réguliers et irréguliers, ainsi que des prismes convexes et concaves.

Références
- Billstein, R., Libeskind, S. et Lott, J. W. (2013). Mathématiques: une approche de résolution de problèmes pour les enseignants de l'éducation de base. López Mateos Editores.
- Fregoso, R. S. et Carrera, S. A. (2005). Mathématiques 3. Progress Editorial.
- Gallardo, G. et Pilar, P. M. (2005). Mathématiques 6. Progress Editorial.
- Gutiérrez, C. T. et Cisneros, M. P. (2005). Cours de mathématiques 3ème Progress Editorial.
- Kinsey, L. et Moore, T. E. (2006). Symétrie, forme et espace: une introduction aux mathématiques par la géométrie (illustré, réimpression éd.). Springer Science & Business Media.
- Mitchell, C. (1999). Conceptions de lignes mathématiques éblouissantes (Éditeur illustré). Scholastic Inc.
- R., M. P. (2005). Je dessine 6ème. Progress Editorial.



 Prisme quadrangulaire
Prisme quadrangulaire Prisme hexagonal
Prisme hexagonal