Quels sont les 3 éléments d'un vecteur?
Le éléments d'un vecteur ils sont l'adresse, la distance et le module. En mathématiques, en physique et en ingénierie, un vecteur est un objet géométrique ayant une magnitude (ou une longueur) et une direction. Selon l'algèbre vectorielle, les vecteurs peuvent être ajoutés à d'autres vecteurs.
Fréquemment, un vecteur est représenté par un segment de ligne avec une direction définie, ou représenté graphiquement sous la forme d'une flèche, reliant un point initial A à un point terminal B, désigné par AB.
Un vecteur est ce qui est nécessaire pour amener le point A au point B. Les vecteurs jouent un rôle important en physique: la vitesse et l'accélération d'un objet en mouvement et les forces qui y agissent peuvent être décrites avec des vecteurs.
De nombreuses autres qualités physiques peuvent être considérées comme des vecteurs. La représentation mathématique d'un vecteur physique dépend du système de coordonnées utilisé pour le décrire.
Il existe plusieurs classes de vecteurs, parmi lesquels on peut trouver des vecteurs glissants, des vecteurs colinéaires, des vecteurs concurrents, des vecteurs de position, des vecteurs libres, des vecteurs parallèles et des vecteurs coplanaires, entre autres.
Éléments d'un vecteur
Principalement un vecteur a trois éléments: la direction, le sens et le module.
adresse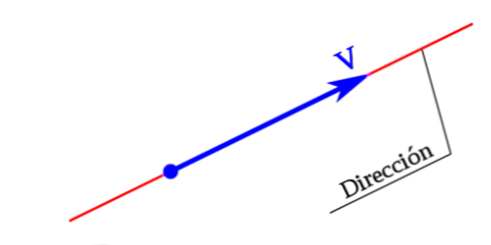
Un vecteur est une entité qui a une ampleur et une direction. Des exemples de vecteurs comprennent le déplacement, la vitesse, l'accélération et la force.
Pour décrire l'une de ces grandeurs vectorielles, il est nécessaire de trouver l'ampleur et la direction.
Par exemple, si la vitesse d'un objet est de 25 mètres par seconde, la description de la vitesse de l'objet est incomplète, puisque l'objet peut se déplacer à 25 mètres par seconde vers le sud ou à 25 mètres par seconde vers le nord, ou 25 mètres par seconde au sud-est.
Pour décrire complètement la vitesse d'un objet, il faut définir les deux: la magnitude de 25 mètres par seconde et la direction, par exemple au sud.
Pour que de telles descriptions de quantités vectorielles soient utiles, il est important que tout le monde s'accorde sur la description de la direction de l'objet.
La plupart des gens sont habitués à l'idée que la direction est sur une carte si vous regardez à droite. Mais il s’agit d’une simple convention que les cartographes utilisent depuis des années pour que tout le monde soit d’accord.
Alors, quelle est la direction d'une quantité vectorielle qui ne va pas au nord ou à l'est, sinon entre le nord et l'est? Pour ces cas, il est important qu'il existe une convention pour décrire la direction dudit vecteur.
Cette convention est appelée CCW. En utilisant cette convention, nous pouvons décrire la direction de tout vecteur en termes d’angle de rotation à gauche.
En utilisant cette convention, la direction nord serait à 90 °, car si un vecteur pointe vers l'est, il devrait être tourné de 90 ° vers la gauche pour atteindre le point nord.
En outre, la direction vers l’ouest serait située à 180 °, puisqu'un vecteur pointant vers l’ouest devrait être tourné de 180 ° vers la gauche pour indiquer le point ouest.
En d'autres termes, la direction d'un vecteur sera représentée par une ligne contenue dans le vecteur ou par toute ligne qui lui est parallèle,
Il sera déterminé par l'angle formé entre le vecteur et toute autre ligne de référence. C'est-à-dire que la direction de la ligne qui se trouve dans le vecteur ou une ligne parallèle à celle-ci est la direction du vecteur.
Sens
La signification du vecteur fait référence à l'élément qui décrit comment le point A va à la fin B:

Le sens d'un vecteur est spécifié par l'ordre de deux points sur une ligne parallèle au vecteur, contrairement à la direction du vecteur spécifiée par la relation entre le vecteur et une ligne de référence et / ou un plan.
La direction et le sens déterminent la direction d'un vecteur. L'orientation indique l'angle dans lequel se trouve le vecteur et le sens indique où il pointe.

La direction du vecteur n'établit que l'angle que fait un vecteur avec son axe horizontal, mais cela peut créer une ambiguïté puisque la flèche peut pointer dans deux directions opposées tout en conservant le même angle.
Le sens clarifie cette ambiguïté et indique où la flèche pointe ou où se trouve le vecteur.
D'une certaine manière, le sens nous indique l'ordre dans lequel lire le vecteur. Indiquez où le vecteur commence et où il se termine.
Module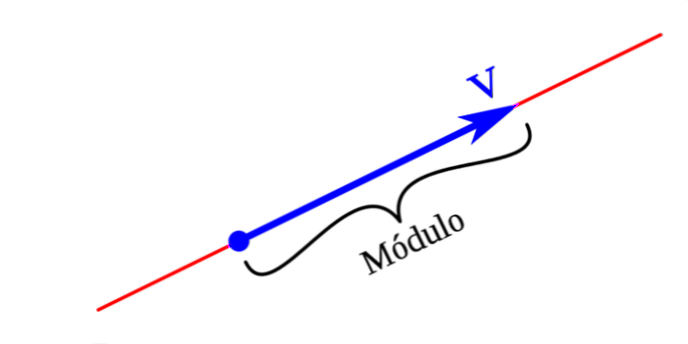
Le module ou l'amplitude d'un vecteur peut être défini comme la longueur du segment AB. Le module peut être représenté par une longueur proportionnelle à la valeur du vecteur. Le module d'un vecteur sera toujours nul ou, dans d'autres cas, un nombre positif.
En mathématiques, le vecteur sera défini par sa distance euclidienne (module), sa direction et son sens.
La distance euclidienne ou distance euclidienne est la distance «ordinaire» en ligne droite entre deux points situés dans un espace euclidien. Avec cette distance, l'espace euclidien devient un espace métrique.
Une distance euclidienne entre deux points, par exemple P et Q, est la distance entre le segment de ligne qui les relie:

La position d'un point dans un espace euclidien n est un vecteur. Ainsi, P et Q sont des vecteurs, à partir de l'origine de l'espace et leurs points indiquant deux points.
La norme euclidienne, la magnitude ou la distance euclidienne d'un vecteur mesurent la longueur dudit vecteur.
Références
- Direction de vecteur. Récupéré de physicsclassroom.com.
- Quel est le sens d'un vecteur? Récupéré de physics.stackexchange.com.
- Quelle est la différence entre la direction, le sens et l'orientation? Récupéré de math.stackexchange.com.
- Distance euclidienne. Récupéré de wikipedia.org.




